Grand Mont Hall Consider A Nonstochastic One Good Overlapping Generations Model Cons 1946843
Grand mont-Hall Consider a nonstochastic, one-good overlapping generations model consisting of two-period-lived young people born in each t ≥ 1 and an initial group of old people at t = 1 who are endowed with H(0) > 0 units of unbacked currency at the beginning of period 1. The one good in the model is not storable. Let the aggregate first-period saving function of the young be time invariant and be denoted f[1 + r(t)] where [1+r(t)] is the gross rate of return on consumption loans between t and (t + 1). The saving function is assumed to satisfy f(0) = −∞, f (1 + r) > 0, f(1) > 0. Let the government pay interest on currency, starting in period 2 (to holders of currency between periods 1 and 2). The government pays interest on currency at a nominal rate of [1 + r(t)]p(t + 1)/p, where [1 + r(t)] is the real gross rate of return on consumption loans, p(t) is the price level at t, and ¯p is a target price level chosen to satisfy
![]()
The government finances its interest payments by printing new money, so that the government’s budget constraint is
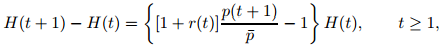
Given H(1) = H(0) > 0. The gross rate of return on consumption loans in this economy is 1 + r(t). In equilibrium, [1 + r(t)] must be at least as great as the real rate of return on currency
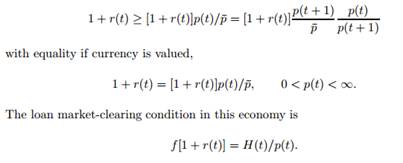
a. Define an equilibrium.
b. Prove that there exists a unique monetary equilibrium in this economy and compute it.

